Speed of Mini-Batch SGD

This post comes from a friend’s question, that he says sometimes mini-batch SGD converges more slowly than single SGD.

Let’s begin with what these two kinds of method are and where they differ. Here notice that mini-batch methods come from batch methods.

##Batch gradient descent

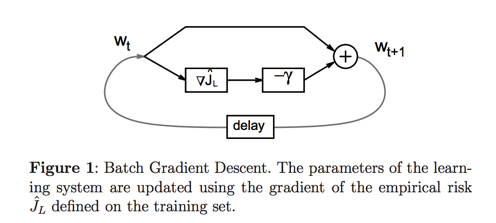
Batch gradient descent computes the gradient using the whole dataset, while Stochastic gradient descent (SGD) computes the gradient using a single sample. This is great for convex, or relatively smooth error manifolds. In this case, we move directly towards an optimum solution, either local or global.

###pros

1. Great for convex, or relatively smooth error manifolds because it directly towards to the optimum solution.

###cons

1. Using the whole dataset means that it is updating the parameters using all the data. Each iteration of the batch gradient descent involves a computation of the average of the gradients of the loss function over the entire training data set. So the computation cost matters.

##Stochastic gradient descent

While Batch gradient descent computes the gradient using the whole dataset, Stochastic gradient descent (SGD) computes the gradient using a single sample.

###pros

1. Obviously SGD’s computationally a whole lot faster.

2. Single SGD works well better than batch gradient descent when the error manifolds that have lots of local maxima/minima.

###cons

1. Sometimes, with the computational advantage, it should perform many more iterations of SGD, making many more steps than conventional batch gradient descent.

##mini-batch SGD

There comes the compromise of this two kinds of methods. When the batch size is 1, it is called stochastic gradient descent (GD). When you set the batch size to 10 or to some extend larger, this method is called mini-batch SGD. Mini-batch performs better than true stochastic gradient descent because when the gradient computed at each step uses more training examples, mini-batches tend to average a little of the noise out that single samples inherently bring. Thus, the amount of noise is reduced when using mini-batches. Therefore, we usually see smoother convergence out of local minima into a more optimal region.

Thus, the batch size matters for the balance. We primally want the size to be small enough to avoid some of the poor local minima, and large enough that it doesn’t avoid the global minima or better-performing local minima. Also, a pratical consideratio raises from tractability that each sample or batch of samples must be loaded in a RAM-friendly size.

So let’s be more clear:

##Why should we use mini-batch?

1. It is small enough to let us implement vectorization in RAM.
2. Vectorization brings efficiency.

##Disadvantage of mini-batch SGD is the difficulty in balancing the batch size \(b\).

However, in the paper Sample size selection in optimization methods for machine learning, the author points out that though large mini-batches are preferable to reduce the communication cost, they may slow down convergence rate in practice. And Mu Li in this papar is dealing with this problem.

##Ref

[1]Bottou, Léon. Large-scale machine learning with stochastic gradient descent. Proceedings of COMPSTAT’2010. Physica-Verlag HD, 2010. 177-186.

[2]Bottou, Léon. Online learning and stochastic approximations. On-line learning in neural networks 17.9 (1998): 142.

[3]Li, Mu, et al. Efficient mini-batch training for stochastic optimization. Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2014.